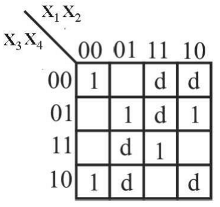
Consider the Karnaugh map given below : The function represented by this map can be simplified to the minimal form as

A. $${{\text{x}}_1}{\overline {\text{x}} _2}{\overline {\text{x}} _4} + {{\text{x}}_2}{{\text{x}}_4} + {{\text{x}}_1}{\overline {\text{x}} _3}$$

B. $${{\text{x}}_1}{{\text{x}}_2}{{\text{x}}_4} + {{\text{x}}_2}{{\text{x}}_4} + {{\text{x}}_1}{\overline {\text{x}} _2}{\overline {\text{x}} _3}{\overline {\text{x}} _4}$$

C. $${{\text{x}}_2}{{\text{x}}_4} + {\overline {\text{x}} _2}{\overline {\text{x}} _4} + {{\text{x}}_1}{\overline {\text{x}} _3}$$

D. $${{\text{x}}_1}{\overline {\text{x}} _2}{\overline {\text{x}} _4} + {\overline {\text{x}} _1}{{\text{x}}_2}{\overline {\text{x}} _3}{{\text{x}}_4} + {{\text{x}}_1}{{\text{x}}_2}$$

Answer: Option C