1. A 1.0 kHz signal is flat top sampled at the rate of 1800 samples/sec and the samples are applied to an ideal rectangular LPF with cut-off frequency of 1100 Hz, then the output of the filter contains
2. A 4 GHz carrier is DSB-SC modulated by a low pass message signal with maximum frequency of 2 MHz. The resultant signal is to be ideally sampled. The minimum frequency of the sampling impulse train should be
3. Increased pulse width in the flat top sampling, leads to
4. A video transmission system transmits 625 picture frames per second. Each frame consists of a 400 × 400 pixel grid with 64 intensity levels per pixel. The data rate of the system is
5. The raised cosine pulse p(t) is used for zero ISI in digital communications. The expression for p(t) with unity roll-off factor is given by $$p\left( t \right) = \frac{{\sin 4\pi \omega t}}{{4\pi \omega t\left( {1 - 16{\omega ^2}{t^2}} \right)}}.$$ The value of p(t) at $$t = \frac{1}{{4\omega }}$$ is
6. A sinusoidal signal of 2 kHz frequency is applied to a delta modulator. The sampling rate and step-size Δ of the delta modulator are 20,000 samples per second and 0.1 V, respectively. To prevent slope overload, the maximum amplitude of the sinusoidal signal (in Volts) is
7. Coherent orthogonal binary FSK modulation is used to transmit two equiprobable symbol waveforms s1(t) = αcos2πf1t & s2(t) = αcos2πf2t1 where α = 4 mV. Assume an AWGN channel with two-sided noise power spectral density $$\frac{{{N_0}}}{2} = 0.5 \times {10^{ - 12}}W/Hz.$$ Using an optimal receiver and the relation $$Q\left( v \right) = \frac{1}{{\sqrt {2\pi } }}\int\limits_v^\infty {{\theta ^{\frac{{{u^2}}}{2}}}du,} $$ the bit error probability for a data rate of 500 kbps is
8. During transmission over a certain binary communication channel, bit errors occur independently with probability p. The probability of AT MOST one bit in error in a block of n bits is given by
9. The message bit sequence to a DPSK modulator is 1, 1, 0, 0, 1, 1. The carrier phase during the reception of the first two message bits is π, π. The carrier phase for the remaining four message bits is
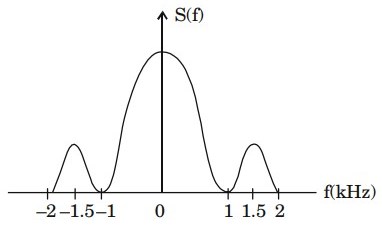
10. A deterministic signal has the power spectrum given in figure. The minimum sampling rate needed to completely represent signal is