61. Match List-I with List-II in regard to Fourier series of periodic f(t) and select the correct answer using the options given below:
List-I (Properties)
List-II (Characteristics of the trigonometric form)
a. f(t) + f(-t) = 0
1. Even harmonics can exist
b. f(t) - f(-t) = 0
2. Odd harmonics can exist
c. $${\text{f}}\left( {\text{t}} \right) + {\text{f}}\left( {{\text{t}} - \frac{{\text{T}}}{2}} \right) = 0$$
3. The dc and cosine terms can exist
d. $${\text{f}}\left( {\text{t}} \right) - {\text{f}}\left( {{\text{t}} - \frac{{\text{T}}}{2}} \right) = 0$$
4. sine terms can exist
5. cosine terms of even harmonics can exist
| List-I (Properties) | List-II (Characteristics of the trigonometric form) |
| a. f(t) + f(-t) = 0 | 1. Even harmonics can exist |
| b. f(t) - f(-t) = 0 | 2. Odd harmonics can exist |
| c. $${\text{f}}\left( {\text{t}} \right) + {\text{f}}\left( {{\text{t}} - \frac{{\text{T}}}{2}} \right) = 0$$ | 3. The dc and cosine terms can exist |
| d. $${\text{f}}\left( {\text{t}} \right) - {\text{f}}\left( {{\text{t}} - \frac{{\text{T}}}{2}} \right) = 0$$ | 4. sine terms can exist |
| 5. cosine terms of even harmonics can exist |
62. Find the sampling frequency (fs) in the below figure?
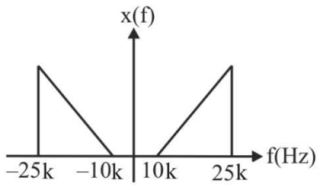

63. The poles of a digital filter with linear phase response can lie
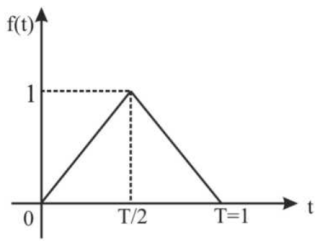
64. Laplace transform of the function f(t) shown in the figure is

65. A continuous time LTI system is described by $$\frac{{{d^2}y\left( t \right)}}{{d{t^2}}} + 4\frac{{dy\left( t \right)}}{{dt}} + 3y\left( t \right) = 2\frac{{dx\left( t \right)}}{{dt}} + 4x\left( t \right)$$
Assuming zero initial conditions, the response y(t) of the above system for the input x(t) = e-2tu(t) is given by
Assuming zero initial conditions, the response y(t) of the above system for the input x(t) = e-2tu(t) is given by
66. A periodic triangular wave is shown in the figure. Its Fourier components will consist only of

67. A discrete time, which is both linear and time invariant, the impulse response is u[n]. What is the response of the system for an input δ[n - 4]?
68. The impulse response of a discrete system with a simple pole is shown in the given figure
The pole must be located
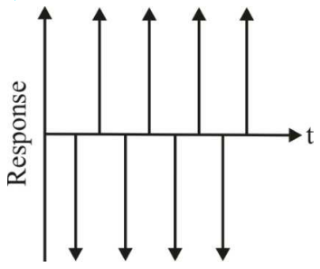
The pole must be located

69. The impulse response of a continuous time system is given by h(t) = δ(t - 1) + δ(t - 3). The value of the step response at t = 2 is
70. A time invariant system is a system whose output
Read More Section(Signal Processing)
Each Section contains maximum 100 MCQs question on Signal Processing. To get more questions visit other sections.
