61. A periodic signal x(t) has a trigonometric Fourier series expansion $$x\left( t \right) = {a_0} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\cos n{\omega _0}t + {b_n}\sin n{\omega _0}t} \right)} $$
If $$x\left( t \right) = - x\left( { - t} \right) = - x\left( {t - \frac{\pi }{{{\omega _0}}}} \right),$$ we can conclude that
If $$x\left( t \right) = - x\left( { - t} \right) = - x\left( {t - \frac{\pi }{{{\omega _0}}}} \right),$$ we can conclude that
62. The transfer function of a linear system is the
63. Match List-I with List-II and select the correct answer using the options given below:
List-I (Function)
List-II (Fourier Transforms)
a. $$\exp \left( { - \alpha t} \right)u\left( t \right),\,\alpha > 0$$
1. $$\frac{1}{{{{\left( {\alpha + j2\pi f} \right)}^2}}}$$
b. $$\exp \left( { - \alpha \left| t \right|} \right),\,\alpha > 0$$
2. $$\frac{1}{{\alpha + j2\pi f}}$$
c. $${\text{texp}}\left( { - \alpha t} \right)u\left( t \right),\,\alpha > 0$$
3. $$\delta \left( {f - \frac{\alpha }{{{t_0}}}} \right)$$
d. $$\exp \left( {j2\pi \alpha t/{t_0}} \right)$$
4. $$\frac{{2\alpha }}{{{\alpha ^2} + {{\left( {2\pi f} \right)}^2}}}$$
| List-I (Function) | List-II (Fourier Transforms) |
| a. $$\exp \left( { - \alpha t} \right)u\left( t \right),\,\alpha > 0$$ | 1. $$\frac{1}{{{{\left( {\alpha + j2\pi f} \right)}^2}}}$$ |
| b. $$\exp \left( { - \alpha \left| t \right|} \right),\,\alpha > 0$$ | 2. $$\frac{1}{{\alpha + j2\pi f}}$$ |
| c. $${\text{texp}}\left( { - \alpha t} \right)u\left( t \right),\,\alpha > 0$$ | 3. $$\delta \left( {f - \frac{\alpha }{{{t_0}}}} \right)$$ |
| d. $$\exp \left( {j2\pi \alpha t/{t_0}} \right)$$ | 4. $$\frac{{2\alpha }}{{{\alpha ^2} + {{\left( {2\pi f} \right)}^2}}}$$ |
64. The Fourier Transform of a function x(t) is X(f). The Fourier transform of $$\frac{{dx\left( t \right)}}{{dt}}$$ will be
65. A finite duration discrete-time signal x(n) is obtained by sampling the continuous-time signal x(t) = cos(200πt) at sampling instant t = n/400, n = 0, 1, . . . , 7. The 8-point discrete Fourier transform (DFT) of x(n) is defined as $$X\left[ k \right] = \sum\limits_{n = 0}^7 {x\left[ n \right]{e^{\frac{{ - j\pi kn}}{4}}},\,k = 0,\,1,\,.....,\,7} $$
Which one of the following statements is true?
Which one of the following statements is true?
66. In inverse DTFT, the . . . . . . . . is defined between -π to π because of the property.
67. If random process X(t) and Y(t) are orthogonal then
68. Consider a system whose input x and output y are related by the equation
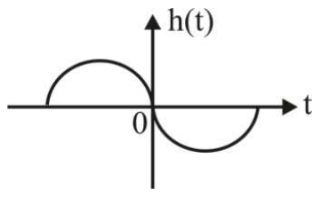
$$y\left( t \right) = \int\limits_{ - \infty }^\infty {x\left( {t - \tau } \right)h\left( {2\tau } \right)d\tau } $$
where h(t) is shown in the graph
Which of the following four properties are possessed by the system?
BIBO: Bounded input gives a bounded output
Causal : The system is causal
LP : The system is low pass
LTI : The system is linear and time-invariant
$$y\left( t \right) = \int\limits_{ - \infty }^\infty {x\left( {t - \tau } \right)h\left( {2\tau } \right)d\tau } $$
where h(t) is shown in the graph
Which of the following four properties are possessed by the system?
BIBO: Bounded input gives a bounded output
Causal : The system is causal
LP : The system is low pass
LTI : The system is linear and time-invariant

69. Which of the following is the correct statement?
The region of the convergence of z-transform of x[n] consists of the value of z for which x[n]r-n is
The region of the convergence of z-transform of x[n] consists of the value of z for which x[n]r-n is
70. About the Fourier series expansion of a periodic function it can be said that
Read More Section(Signal Processing)
Each Section contains maximum 100 MCQs question on Signal Processing. To get more questions visit other sections.
