From the top of a cliff 25 m high the angle of elevation of a tower is found to be equal to the angle of depression of the foot of the tower. The height of the tower is

Solution(By Examveda Team)

Let AB be the tower and CD be cliff Angle of elevation of A is equal to the angle of depression of B at C
Let angle be Q and CD = 25 m

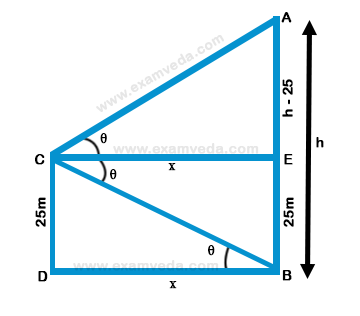
$$\eqalign{ & {\text{Let}}\,AB = h \cr & CE \,\, || \,\, DB \cr & \therefore EC = DB = x{\text{ }}\left( {{\text{suppose}}} \right) \cr & EB = CD = 25 \cr & \therefore AE = h - 25 \cr & {\text{Now in right }}\Delta CDB, \cr & \tan \theta = \frac{{CD}}{{DB}} = \frac{{25}}{x}\,......\left( {\text{i}} \right) \cr & {\text{and in right }}\Delta CAE \cr & \tan \theta = \frac{{AE}}{{CE}} = \frac{{h - 25}}{x}\,......\left( {{\text{ii}}} \right) \cr & {\text{From}}\left( {\text{i}} \right){\text{ and }}\left( {{\text{ii}}} \right) \cr & \frac{{25}}{x} = \frac{{h - 25}}{x} \cr & \Rightarrow 25 = h - 25 \cr & \Rightarrow h = 25 + 25 = 50 \cr & \therefore {\text{Height of tower}} = 50\,m \cr} $$