From the top of a hill 100 m high, the angles of depression of the top and bottom of a pole are 30° and 60° respectively. What is the height of the pole?

Solution(By Examveda Team)

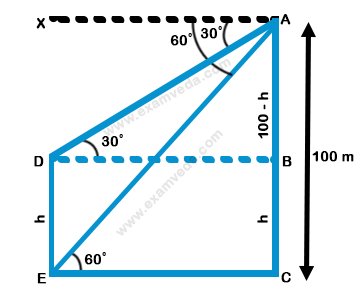
Consider the diagram shown above. AC represents the hill and DE represents the pole
Given that AC = 100 m
∠XAD = ∠ADB = 30° (∵ AX || BD )
∠XAE = ∠AEC = 60° (∵ AX || CE)

Let DE = h

Then, BC = DE = h,
AB = (100 - h)   (∵ AC = 100 and BC = h),
BD = CE
$$\eqalign{ & \tan {60^ \circ } = \frac{{AC}}{{CE}} \cr & \Rightarrow \sqrt 3 = \frac{{100}}{{CE}} \cr & \Rightarrow CE = \frac{{100}}{{\sqrt 3 }}\,......\left( 1 \right) \cr & \tan {30^ \circ } = \frac{{AB}}{{BD}} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{{100 - h}}{{BD}} \cr} $$
$$ \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{{100 - h}}{{\left( {\frac{{100}}{{\sqrt 3 }}} \right)}}$$      (∵ BD = CE and substituted the value of CE from eq. 1)
$$\eqalign{ & \Rightarrow \left( {100 - h} \right) = \frac{1}{{\sqrt 3 }} \times \frac{{100}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{100}}{3} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 33.33 \cr & \Rightarrow h = 100 - 33.33 = 66.67\,{\text{m}} \cr} $$
i.e., the height of the pole = 66.67 m