If the angle of elevation of a tower from a distance of 100 metres from its foot is 60?, the height of the tower is

Solution(By Examveda Team)

Let AB be the tower and a point P at a distance of 100 m from its foot, angle of elevation of the top of the tower is 60°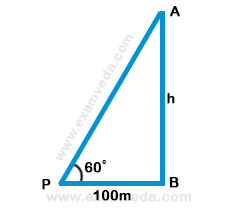

Let height of the tower = h
$$\eqalign{ & {\text{Then in right }}\Delta ABP \cr & \tan \theta = \frac{{{\text{Perpendicular}}}}{{{\text{Base}}}} = \frac{{AB}}{{PB}} \cr & \Rightarrow \tan {60^ \circ } = \frac{h}{{100}} \Rightarrow \sqrt 3 = \frac{h}{{100}} \cr & \Rightarrow h = 100\sqrt 3 \cr & \therefore {\text{Height}}\,{\text{of}}\,{\text{tower}} = 100\sqrt 3 \cr} $$