In a triangle ABC, a line XY is drawn parallel to BC meeting AB in X and AC in Y. The area of the triangle AXY is half of the area of the triangle ABC. XY divides AB in the ratio of :

Solution(By Examveda Team)

Note : The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
Since, XY || BC, we have :

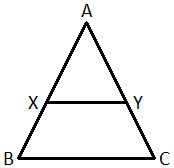
$$\eqalign{ & \angle AXY = \angle ABC{\text{ and }} \cr & \angle AYX = \angle ACB \cr & {\text{Aslo, }}\angle A = \angle A\,\,{\text{(common)}} \cr & {\text{So, }}\vartriangle AXY \sim \,\vartriangle ABC \cr & {\text{Let area (}}\vartriangle ABC{\text{)}} = x\,\text{sq. units} \cr & {\text{Then,}} \cr & {\text{Area (}}\vartriangle AXY{\text{) = }}\frac{x}{2}\text{sq. units} \cr & \frac{{{{\left( {AB} \right)}^2}}}{{{{\left( {AX} \right)}^2}}} = \frac{x}{{\left( {\frac{x}{2}} \right)}} \cr & \Rightarrow \frac{{AB}}{{AX}} = \sqrt 2 \cr & \Rightarrow \frac{{AX + BX}}{{AX}} = \sqrt 2 \cr & \Rightarrow 1 + \frac{{BX}}{{AX}} = \sqrt 2 \cr & \Rightarrow \frac{{BX}}{{AX}} = \left( {\sqrt 2 - 1} \right) \cr & \Rightarrow \frac{{AX}}{{BX}} = \frac{1}{{\left( {\sqrt 2 - 1} \right)}}{\text{ Or 1}}:\left( {\sqrt 2 - 1} \right) \cr} $$