1. The ratio between the length and the breadth of a rectangular park is 3 : 2. If a man cycling along the boundary of the park at the speed of 12 km/hr completes one round in 8 minutes, then the area of the park (in sq. m) is:
2. An error 2% in excess is made while measuring the side of a square. The percentage of error in the calculated area of the square is:
3. The ratio between the perimeter and the breadth of a rectangle is 5 : 1. If the area of the rectangle is 216 sq. cm, what is the length of the rectangle?
4. The percentage increase in the area of a rectangle, if each of its sides is increased by 20% is:
5. A rectangular park 60 m long and 40 m wide has two concrete crossroads running in the middle of the park and rest of the park has been used as a lawn. If the area of the lawn is 2109 sq. m, then what is the width of the road?
6. The diagonal of the floor of a rectangular closet is $$7\frac{1}{2}$$ feet. The shorter side of the closet is $$4\frac{1}{2}$$ feet. What is the area of the closet in square feet?
7. A towel, when bleached, was found to have lost 20% of its length and 10% of its breadth. The percentage of decrease in area is:
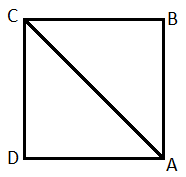
8. A man walked diagonally across a square lot. Approximately, what was the percent saved by not walking along the edges?
9. The diagonal of a rectangle is $$\sqrt {41} $$ cm and its area is 20 sq. cm. The perimeter of the rectangle must be:
10. What is the least number of squares tiles required to pave the floor of a room 15 m 17 cm long and 9 m 2 cm broad?
Read More Section(Area)
Each Section contains maximum 100 MCQs question on Area. To get more questions visit other sections.