In the given diagram, ABCD is a square and semi-circular regions have been added to it by drawing two semi-circles with AB and CD as diameters. If the total area of the three regions is 350 sq.cm, then the length of the side of the square is equal to : 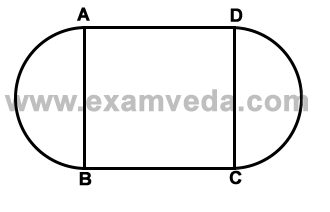
A. $$5\sqrt 7 $$ cm
B. 7 cm
C. 13 cm
D. 14 cm
Answer: Option D
Solution (By Examveda Team)
Let the length of the side of the square be x cmThen, radius of each semi-circle = $$\left( {\frac{x}{2}} \right)$$ cm
Total area :
$$\eqalign{ & = \left[ {{x^2} + \frac{\pi }{2}{{\left( {\frac{x}{2}} \right)}^2} + \frac{\pi }{2}{{\left( {\frac{x}{2}} \right)}^2}} \right]c{m^2} \cr & = \left( {{x^2} + \frac{\pi }{4} \times {x^2}} \right)c{m^2} \cr} $$
$$\eqalign{ & \therefore {x^2} + \frac{\pi }{4} \times {x^2} = 350 \cr & \Rightarrow {x^2} + \frac{{22{x^2}}}{{28}} = 350 \cr & \Rightarrow {x^2} + \frac{{11{x^2}}}{{14}} = 350 \cr & \Rightarrow \frac{{25{x^2}}}{{14}} = 350 \cr & \Rightarrow {x^2} = \left( {\frac{{350 \times 14}}{{25}}} \right) \cr & \Rightarrow {x^2} = 196 \cr & \Rightarrow x = 14\,cm \cr} $$
Related Questions on Area
A. 15360 m2
B. 153600 m2
C. 30720 m2
D. 307200 m2
E. None of these
A. 2%
B. 2.02%
C. 4%
D. 4.04%
E. None of these
A. 16 cm
B. 18 cm
C. 24 cm
D. Data inadequate
E. None of these

Join The Discussion