1. When the wavelength of the incident X-Tay increases the angle of diffraction
2. Identify the false statement.
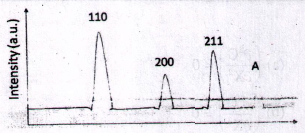
3. A schematic of X-ray diffraction pattern of a single phase cubic polycrystal is given below. The miller idices of Peak A is

4. The theoretical density of an fcc metal with atomic radius and atomic weight of 0.144 nm and 197 gm.mol-1 respectively, is approximately (in kg.m-3)
5. A simplified energy band-diagram of an intrinsic semiconductor at thermal equilibrium (300 K) is shown. In the accompanying table, which one of the four cloumns correctly represents the listed parameters? Assume same effective mass for electrons and holes.

Parameter
Energy-difference
Column 1
Column 2
Column 3
Column 4
Band-gap
ΔE2
ΔE1
ΔE2
ΔE1
Electron affinity
$$\frac{{\Delta {E_1}}}{2}$$
ΔE2 - ΔE1
$$\frac{{\Delta {E_2}}}{2}$$
ΔE2 - $$\left( {\frac{{\Delta {E_1}}}{2}} \right)$$
Work function
ΔE1 + ΔE2
ΔE2 - $$\left( {\frac{{\Delta {E_1}}}{2}} \right)$$
ΔE1 - $$\frac{{\Delta {E_2}}}{2}$$
ΔE2 + $$\left( {\frac{{\Delta {E_1}}}{2}} \right)$$

| Parameter | Energy-difference | |||
| Column 1 | Column 2 | Column 3 | Column 4 | |
| Band-gap | ΔE2 | ΔE1 | ΔE2 | ΔE1 |
| Electron affinity | $$\frac{{\Delta {E_1}}}{2}$$ | ΔE2 - ΔE1 | $$\frac{{\Delta {E_2}}}{2}$$ | ΔE2 - $$\left( {\frac{{\Delta {E_1}}}{2}} \right)$$ |
| Work function | ΔE1 + ΔE2 | ΔE2 - $$\left( {\frac{{\Delta {E_1}}}{2}} \right)$$ | ΔE1 - $$\frac{{\Delta {E_2}}}{2}$$ | ΔE2 + $$\left( {\frac{{\Delta {E_1}}}{2}} \right)$$ |
