The altitude of an equilateral triangle of side $$2\sqrt 3 $$ cm is :

A. $$\frac{1}{2}$$ cm

B. $$\frac{{\sqrt 3 }}{4}$$ cm

C. $$\frac{{\sqrt 3 }}{2}$$ cm

D. 3 cm

Answer: Option D

Solution(By Examveda Team)

Let ABC be the equilateral triangle and AD be the altitude on base BC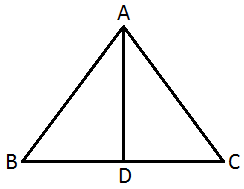

In an equilateral triangle, the altitude and the median coincide.
So, BC = DC = $$\left( {\frac{{2\sqrt 3 }}{2}} \right)$$ cm = $$\sqrt 3 $$ cm
Let the length of the altitude AD be x cm
Then, in right angled ΔADB,
AB² = AD² + BD²
⇒ $${\left( {2\sqrt 3 } \right)^2}$$  = x² + $${\left( {\sqrt 3 } \right)^2}$$
⇒ x² = (12 - 3)
⇒ x² = 9
⇒ x = 3 cm