The angle of elevation of the top of a tower from a certain point is 30°. If the observed moves 20 m towards the tower, the angle of elevation the angle of elevation of top of the tower increases by 15°. The height of the tower is

Solution(By Examveda Team)

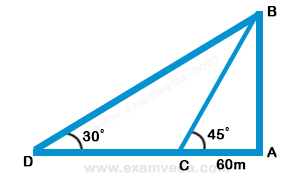
Let AB be the tower and C and D be the points of observation.
Then, ∠ACB = 30°, ∠ADB = 45° and CD = 20m
Let AB = h then,
$$\eqalign{ & \frac{{AB}}{{AC}} = \tan 30^\circ = \frac{1}{{\sqrt 3 }} \cr & \Rightarrow AC = AB \times \sqrt 3 = h\sqrt 3 {\kern 1pt} {\text{And,}} \cr & \Rightarrow \frac{{AB}}{{AD}} = \tan 45^\circ = 1 \cr & \Rightarrow AD = AB = h \cr & \, \, \, \, \, CD = 20 \cr & \Rightarrow \left( {AC - AD} \right) = 20 \cr & \Rightarrow h\sqrt 3 - h = 20 \cr & \therefore h = \frac{{20}}{{\left( {\sqrt 3 - 1} \right)}} \times \frac{{\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 + 1} \right)}} \cr & = 10\left( {\sqrt 3 + 1} \right){\text{m}} \cr & = \left( {10 \times 2.73} \right){\text{m}} \cr & = 27.3 {\text{m}} \cr} $$