The base of an isosceles is 14 cm and its perimeter is 36 cm. Find its area.

Solution (By Examveda Team)

Let each equal side of isosceles triangle be x cm
Perimeter of an isosceles triangle = 36 cm
$$\eqalign{ & \therefore x + x + 14 = 36 \cr & \Rightarrow 2x = 36 - 14 \cr & \Rightarrow x = \frac{{22}}{2} \cr & \Rightarrow x = 11\,cm \cr} $$

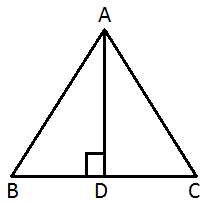
BD = DC = 7cm
From ΔABD
By using Pythagoras theorem :
$$\eqalign{ & AD = \sqrt {A{B^2} - B{D^2}} \cr & \,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {{{11}^2} - {7^2}} \cr & \,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {121 - 49} \cr & \,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {72} \cr & \,\,\,\,\,\,\,\,\,\,\,\, = 3 \times 2\sqrt 2 \cr & \,\,\,\,\,\,\,\,\,\,\,\, = 6\sqrt 2 \,cm \cr} $$
∴ Area of ΔABC
$$\eqalign{ & = \frac{1}{2} \times BC \times AD \cr & = \frac{1}{2} \times 14 \times 6\sqrt 2 \cr & = 42\sqrt 2 {\text{ sq}}{\text{. cm}} \cr} $$