The elevation of the summit of a mountain from its foot is 45°. After ascending 2 km towards the mountain upon an incline of 30°,the elevation changes to 60°. What is the approximate height of the mountain?

Solution(By Examveda Team)

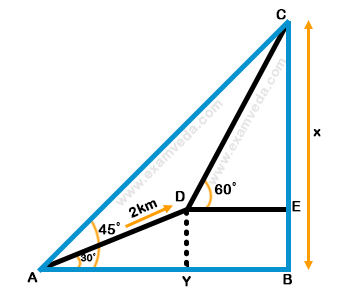
Let A be the foot and C be the summit of a mountain.
Given that ∠CAB = 45°
From the diagram, CB is the height of the mountain. Let CB = x
Let D be the point after ascending 2 km towards the mountain such that AD = 2 km and given that ∠DAY = 30°
It is also given that from the point D, the elevation is 60°
i.e., ∠CDE = 60°
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABC, \cr & \tan {45^ \circ } = \frac{{CB}}{{AB}} \cr} $$
$$ \Rightarrow 1 = \frac{x}{{AB}}$$    [∵ CB = x(the height of the mountain)]
$$\eqalign{ & \Rightarrow AB = x\,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta AYD, \cr & \sin {30^ \circ } = \frac{{DY}}{{AD}} \cr} $$
$$ \Rightarrow \frac{1}{2} = \frac{{DY}}{2}$$    (∵ Given that AD = 2)
$$\eqalign{ & \Rightarrow DY = 1\,.......\left( 2 \right) \cr & \cos {30^ \circ } = \frac{{AY}}{{AD}} \cr} $$
$$ \Rightarrow \frac{{\sqrt 3 }}{2} = \frac{{AY}}{2}$$    (∵ Given that AD = 2)
$$\eqalign{ & \Rightarrow AY = \sqrt 3 \,......\left( 3 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta CED, \cr & \tan {60^ \circ } = \frac{{CE}}{{DE}} \cr} $$
$$ \Rightarrow \tan {60^ \circ } = \frac{{\left( {CB - EB} \right)}}{{YB}}$$     [∵ CE = (CB - EB) and DE = YB)]
$$ \Rightarrow \tan {60^ \circ } = \frac{{\left( {CB - DY} \right)}}{{AB - AY}}$$     [∵ EB = DY and YB = (AB - AY)]
$$ \Rightarrow \tan {60^ \circ } = \frac{{\left( {x - 1} \right)}}{{\left( {x - \sqrt 3 } \right)}}$$
[∵ CB = x, DY = 1(eq:2), AB = x(eq:1) and AY = $${\sqrt 3 }$$ (eq:3)]
$$\eqalign{ & \Rightarrow \sqrt 3 = \frac{{\left( {x - 1} \right)}}{{\left( {x - \sqrt 3 } \right)}} \cr & \Rightarrow x\sqrt 3 - 3 = x - 1 \cr & \Rightarrow x\left( {\sqrt 3 - 1} \right) = 2 \cr & \Rightarrow 0.73x = 2 \cr & \Rightarrow x = \frac{2}{{0.73}} = 2.7 \cr} $$

i.e., the height of the mountain = 2.7 km