The truck of a tree is a right cylinder 1.5 m in radius and 10 m high. The volume of the timber which remains when the truck is trimmed just enough to reduce it to a rectangular parallelopiped on a square base is :

Solution(By Examveda Team)

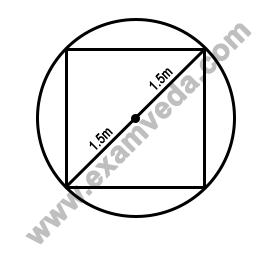
Let the length of each side of the square base be x metres
Then,
$$\eqalign{ & {x^2} + {x^2} = {\left( 3 \right)^2} \cr & \Rightarrow 2{x^2} = 9 \cr & \Rightarrow {x^2} = \frac{9}{2} \cr & \Rightarrow x = \frac{3}{{\sqrt 2 }} \cr} $$
∴ Volume of parallelopiped :
$$\eqalign{ & = \left( {\frac{3}{{\sqrt 2 }} \times \frac{3}{{\sqrt 2 }} \times 10} \right){{\text{m}}^{\text{3}}} \cr & = \frac{{90}}{2}{{\text{m}}^{\text{3}}} \cr & = 45\,{{\text{m}}^{\text{3}}} \cr} $$