To a man standing outside his house, the angles of elevation of the top and bottom of a window are 60° and 45° respectively. If the height of the man is 180 cm and he is 5 m away from the wall, what is the length of the window?

Solution(By Examveda Team)

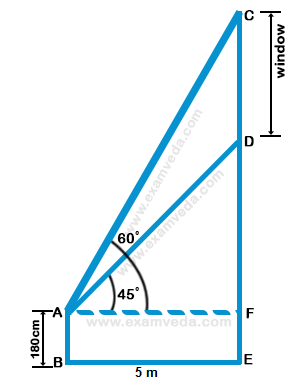
Let AB be the man and CD be the window
Given that the height of the man, AB = 180 cm, the distance between the man and the wall, BE = 5 m,
∠ DAF = 45°, ∠ CAF = 60°
From the diagram, AF = BE = 5 m
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,AFD, \cr & \tan {45^ \circ } = \frac{{DF}}{{AF}} \cr & 1 = \frac{{DF}}{5} \cr & DF = 5\,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,AFC, \cr & \tan {60^ \circ } = \frac{{CF}}{{AF}} \cr & \sqrt 3 = \frac{{CF}}{5} \cr & CF = 5\sqrt 3 \,......\,\left( 2 \right) \cr & {\text{Length}}\,{\text{of}}\,{\text{the}}\,{\text{window}} \cr & = CD = \left( {CF - DF} \right) \cr} $$
  $$ = 5\sqrt 3 - 5$$     [∵ Substituted the value of CF and DF from (1) and (2)]
$$\eqalign{ & = 5\left( {\sqrt 3 - 1} \right) \cr & = 5\left( {1.73 - 1} \right) \cr & = 5 \times 0.73 \cr & = 3.65\,{\text{m}} \cr} $$