Two persons are 'a' meters apart and the height of one is double that of the other. If from the middle point of the line joining their feet, an observer finds the angular elevation of their tops to be complementary, then the height of the shorter post is

Solution(By Examveda Team)

Let AB and CD are two persons standing ‘a’ meters apart
P is the mid-point of BD and from M, the angles of elevation of A and C are complementary

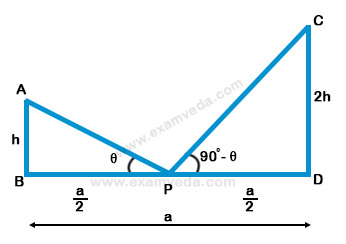
$$\eqalign{ & {\text{In}}\,\,\Delta {\text{APB,}} \cr & \tan \theta = \frac{{AB}}{{BP}} = \frac{h}{{\frac{a}{2}}} = \frac{{2h}}{a} \cr & {\text{In}}\,\,\Delta {\text{CDP,}} \cr & \cot (90 - \theta ) = \frac{{PD}}{{CD}} = \frac{{\frac{a}{2}}}{{2h}} = \frac{a}{{4h}} \cr & {\text{We}}\,\,{\text{Know}}\,\,{\text{that,}} \cr & \tan \theta = \cot (90 - \theta ). \cr & \therefore \frac{{2h}}{a} = \frac{a}{{4h}} \cr & \Rightarrow 8{h^2} = {a^2} \cr & \Rightarrow h = \frac{a}{{2\sqrt 2 }} \cr} $$