Two persons are on either sides of a tower of height 50 m. The persons observers the top of the tower at an angle of elevation of 30° and 60°. If a car crosses these two persons in 10 seconds, what is the speed of the car?

Solution(By Examveda Team)

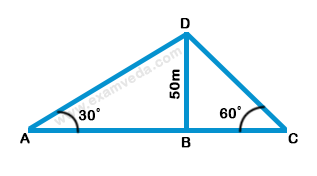
Let BD be the tower and A and C be the positions of the persons.
Given that BD = 50 m, ∠ BAD = 30°, ∠ BCD = 60°
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,ABD, \cr & \tan {30^ \circ } = \frac{{BD}}{{BA}} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{{50}}{{BA}} \cr & \Rightarrow BA = 50\sqrt 3 \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta CBD, \cr & \tan {60^ \circ } = \frac{{BD}}{{BC}} \cr & \Rightarrow \sqrt 3 = \frac{{50}}{{BC}} \cr & \Rightarrow BC = \frac{{50}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{50 \times \sqrt 3 }}{{\sqrt 3 \times \sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{50\sqrt 3 }}{3} \cr} $$
Distance between the two persons
$$\eqalign{ & = AC = BA + BC \cr & = 50\sqrt 3 + \frac{{50\sqrt 3 }}{3} \cr & = \sqrt 3 \left( {50 + \frac{{50}}{3}} \right) \cr & = \frac{{200\sqrt 3 }}{3}\,{\text{m}} \cr} $$
i.e., the distance travelled by the car in 10 seconds = $$\frac{{200\sqrt 3 }}{3}\,{\text{m}}$$
$$\eqalign{ & {\text{Speed}}\,{\text{of the car}} = \frac{{{\text{Distance}}}}{{{\text{Time}}}} \cr & = \frac{{\left( {\frac{{200\sqrt 3 }}{3}} \right)}}{{10}} = \frac{{200\sqrt 3 }}{3}\,{\text{m/s}} \cr & = \frac{{200\sqrt 3 }}{3} \times \frac{{18}}{5}\,{\text{km/hr}} \cr & = {\text{24}}\sqrt 3 \,{\text{km/hr}} \cr} $$