Two poles are ‘a’ metres apart and the height of one is double of the other. If from the middle point of the line joining their feet an observer finds the angular elevations of their tops to be complementary, then the height of the smaller is

Solution(By Examveda Team)

Let height of pole CD = h
and AB = 2h, BD = a
M is mid-point of BD

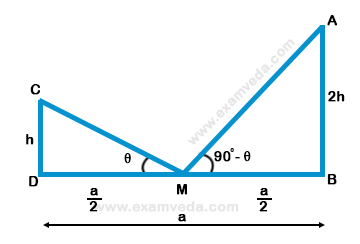
$$\therefore DM = MB = \frac{a}{2}$$
$${\text{Let }}\angle CMD = \theta ,$$    $${\text{then }}\angle AMB = $$     $${90^ \circ } - \theta $$
$$\eqalign{ & {\text{Now}} \cr & \tan \theta = \frac{{CD}}{{DM}} = \frac{h}{{\frac{a}{2}}} = \frac{{2h}}{a}\,......({\text{i}}) \cr & {\text{and}} \cr & tan\left( {{{90}^ \circ } - \theta } \right) = \frac{{AB}}{{MB}} = \frac{{2h}}{{\frac{a}{2}}} = \frac{{4h}}{a} \cr & \Rightarrow \cot \theta = \frac{{4h}}{a}\,..........({\text{ii}}) \cr & {\text{Multiplying (i) and (ii)}} \cr & {\text{tan}}\theta \times {\text{cot}}\theta = \frac{{2h}}{a} \times \frac{{4h}}{a} \cr & 1 = \frac{{8{h^2}}}{{{a^2}}} = {h^2} = \frac{{{a^2}}}{8}\,m \cr & h = \sqrt {\frac{{{a^2}}}{8}} = \frac{a}{{\sqrt 8 }} = \frac{a}{{2\sqrt 2 }}\,m \cr} $$