Two vertical poles are 200 m apart and the height of one is double that of the other. From the middle point of the line joining their feet, an observer finds the angular elevations of their tops to be complementary. Find the heights of the poles.

Solution(By Examveda Team)

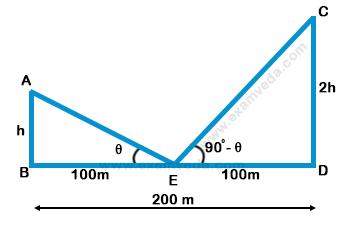
Let AB and CD be the poles with heights h and 2h respectively.
Given that distance between the poles, BD = 200 m
Let E be the middle point of BD,
∠ AEB = $$\theta $$
∠ CED = (90 - $$\theta $$)   (∵ given that angular elevations are complementary)
Since E is the middle point of BD, we have BE = ED = 100 m
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABE, \cr & \tan \theta = \frac{{AB}}{{BE}} \cr & \tan \theta = \frac{h}{{100}} \cr & h = 100\tan \theta \,......\left( 1 \right) \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta EDC, \cr & \tan\left( {90 - \theta } \right) = \frac{{CD}}{{ED}} \cr} $$
$$\cot \theta = \frac{{2h}}{{100}}$$     $$\left[ {\because \tan \left( {90 - \theta } \right) = \cot \theta } \right]$$
$$\eqalign{ & 2h = 100\cot \theta \,......\left( 2 \right) \cr & \left( 1 \right) \times \left( 2 \right) \cr} $$
$$ \Rightarrow 2{h^2} = {100^2}$$     $$\left[ {\because \tan \theta \times \cot\theta = \tan\theta \times \frac{1}{{\tan \theta }} = 1} \right]$$
$$\eqalign{ & \Rightarrow \sqrt 2 \,h = 100 \cr & \Rightarrow h = \frac{{100}}{{\sqrt 2 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{100 \times \sqrt 2 }}{{\sqrt 2 \times \sqrt 2 }} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 50\sqrt 2 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 50 \times 1.41 \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = 70.5 \cr & \Rightarrow 2h = 2 \times 70.5 = 141 \cr} $$
i.e. the height of the poles are 70.5 m and 141 m.