Which among the following sets for Maxwell relation is correct? (U-internal energy, H-enthalpy, A-Helmholtz free energy and G-Gibbs free energy)

A system has two energy levels with energies E and 2E. The lower level is four-fold degenerate while the upper level is doubly degenerate. If there are N non-interacting classical particles in the system, which is in thermodynamic equilibrium at temperature T, the fraction of particles in the upper level is

A. $$\frac{1}{{1 + {e^{ - \varepsilon /{k_B}T}}}}$$

B. $$\frac{1}{{1 + 2{e^{\varepsilon /{k_B}T}}}}$$

C. $$\frac{1}{{2{e^{\varepsilon /{k_B}T}} + 4{e^{2\varepsilon /{k_B}T}}}}$$

D. $$\frac{1}{{2{e^{\varepsilon /{k_B}T}} - 4{e^{2\varepsilon /{k_B}T}}}}$$

A system of non-interacting Fermi particles with Fermi energy E_F has the density of states proportional to √E, where E is the energy of a particle. The average energy per particle at temperature T = 0 is

A. $$\frac{1}{6}{E_F}$$

B. $$\frac{1}{5}{E_F}$$

C. $$\frac{2}{5}{E_F}$$

D. $$\frac{3}{5}{E_F}$$

A piston containing an ideal gas is originally in the state X (see figure). The gas is taken through a thermal cycle X → Y → X as shown

The work done by the gas is positive, if the direction of the thermal cycle is

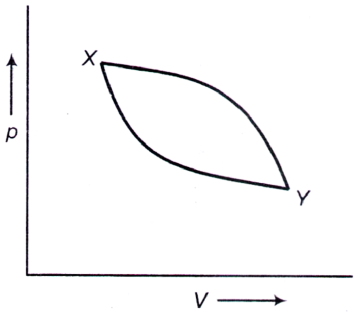
A. clockwise

B. counter-clockwise

C. neither clockwise nor counter-clockwise

D. clockwise from X → Y and counter-clockwise from Y → X

A photon gas is at thermal equilibrium at temperature T. The mean number of photons in an energy state $$\varepsilon = h\omega $$  is

A. $$\exp \left( {\frac{{\hbar \omega }}{{{k_B}T}}} \right) + 1$$

B. $$\exp \left( {\frac{{\hbar \omega }}{{{k_B}T}}} \right) - 1$$

C. $${\left[ {\exp \left( {\frac{{\hbar \omega }}{{{k_B}T}}} \right) + 1} \right]^{ - 1}}$$

D. $${\left[ {\exp \left( {\frac{{\hbar \omega }}{{{k_B}T}}} \right) - 1} \right]^{ - 1}}$$