Thermodynamics and Statistical Physics MCQs Question and Answer in Engineering Physics

1

A system has two energy levels with energies E and 2E. The lower level is four-fold degenerate while the upper level is doubly degenerate. If there are N non-interacting classical particles in the system, which is in thermodynamic equilibrium at temperature T, the fraction of particles in the upper level is

A) $$\frac{1}{{1 + {e^{ - \varepsilon /{k_B}T}}}}$$ B) $$\frac{1}{{1 + 2{e^{\varepsilon /{k_B}T}}}}$$ C) $$\frac{1}{{2{e^{\varepsilon /{k_B}T}} + 4{e^{2\varepsilon /{k_B}T}}}}$$ D) $$\frac{1}{{2{e^{\varepsilon /{k_B}T}} - 4{e^{2\varepsilon /{k_B}T}}}}$$

Discuss

Answer & Solution

Answer: Option A

No explanation is given for this question. Let's Discuss on Board

2

A system of non-interacting Fermi particles with Fermi energy E_F has the density of states proportional to √E, where E is the energy of a particle. The average energy per particle at temperature T = 0 is

A) $$\frac{1}{6}{E_F}$$ B) $$\frac{1}{5}{E_F}$$ C) $$\frac{2}{5}{E_F}$$ D) $$\frac{3}{5}{E_F}$$

Discuss

Answer & Solution

Answer: Option D

No explanation is given for this question. Let's Discuss on Board

3

A piston containing an ideal gas is originally in the state X (see figure). The gas is taken through a thermal cycle X → Y → X as shown
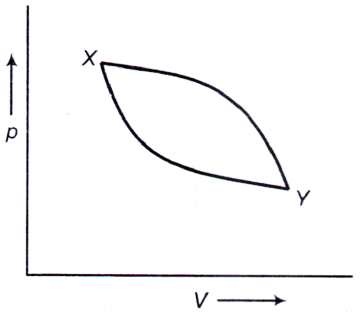
Thermodynamics and Statistical Physics mcq question image

Thermodynamics and Statistical Physics mcq question image

The work done by the gas is positive, if the direction of the thermal cycle is

A) clockwise B) counter-clockwise C) neither clockwise nor counter-clockwise D) clockwise from X → Y and counter-clockwise from Y → X

Discuss

Answer & Solution

Answer: Option A

No explanation is given for this question. Let's Discuss on Board

4

A photon gas is at thermal equilibrium at temperature T. The mean number of photons in an energy state $$\varepsilon = h\omega $$ is

A) $$\exp \left( {\frac{{\hbar \omega }}{{{k_B}T}}} \right) + 1$$ B) $$\exp \left( {\frac{{\hbar \omega }}{{{k_B}T}}} \right) - 1$$ C) $${\left[ {\exp \left( {\frac{{\hbar \omega }}{{{k_B}T}}} \right) + 1} \right]^{ - 1}}$$ D) $${\left[ {\exp \left( {\frac{{\hbar \omega }}{{{k_B}T}}} \right) - 1} \right]^{ - 1}}$$

Discuss

Answer & Solution

Answer: Option D

No explanation is given for this question. Let's Discuss on Board

5

In a classical micro-canonical ensemble for a system of N non-interacting particles, the fundamental volume in phase space which is regarded as equivalent to one micro-state is
(where, h is the Planck's constant.)

A) h^3N B) h^2N C) h^N D) h

Discuss

Answer & Solution

Answer: Option A

No explanation is given for this question. Let's Discuss on Board

6

In the region of co-existence of a liquid and vapour phases of a material

A) C_p and C_V are both infinite B) C_V and $$\beta \left[ { = \frac{1}{V}{{\left( {\frac{{\partial V}}{{\partial T}}} \right)}_p}} \right]$$ are both infinite C) C_V and $$K\left[ { = - \frac{1}{V}{{\left( {\frac{{\partial V}}{{\partial p}}} \right)}_T}} \right]$$ are both infinite D) C_p, β and K are all infinite

Discuss

Answer & Solution

Answer: Option D

No explanation is given for this question. Let's Discuss on Board

7

For a Fermi gas of N particles in three-dimensions at T = 0 K, the Fermi energy E_F is proportional to

A) $${N^{\frac{2}{3}}}$$ B) $${N^{\frac{3}{2}}}$$ C) $${N^3}$$ D) $${N^2}$$

Discuss

Answer & Solution

Answer: Option A

No explanation is given for this question. Let's Discuss on Board

8

The partition function of two Bose particles, each of which can occupy any of the two energy levels 0 and $$\varepsilon $$ is

A) $$1 + {e^{\frac{{ - 2\varepsilon }}{{kT}}}} + 2{e^{\frac{{ - \varepsilon }}{{kT}}}}$$ B) $$1 + {e^{\frac{{ - 2\varepsilon }}{{kT}}}} + {e^{\frac{{ - \varepsilon }}{{kT}}}}$$ C) $$2 + {e^{\frac{{ - 2\varepsilon }}{{kT}}}} + {e^{\frac{{ - \varepsilon }}{{kT}}}}$$ D) $${e^{\frac{{ - 2\varepsilon }}{{kT}}}} + 2{e^{\frac{{ - \varepsilon }}{{kT}}}}$$

Discuss

Answer & Solution

Answer: Option C

No explanation is given for this question. Let's Discuss on Board

9

It is necessary to apply quantum statistics to a system of particles, if

A) there is substantial overlap between the wave functions of the particles B) the mean free path of the particles is comparable to the inter-particle separation C) the particles have identical mass and charge D) the particles are interacting

Discuss

Answer & Solution

Answer: Option D

No explanation is given for this question. Let's Discuss on Board

10

Consider the Fermi-Dirac distribution function f(E) at room temperature (300 K), where E refers tb energy. If E_F is the Fermi energy, which of the following is true?

A) f(E) is a step function B) f(E_F) has a value of $$\frac{1}{2}$$ C) States with E < E_F are filled completely D) f(E) is large and tends to infinity as E decreases much below E_F

Discuss

Answer & Solution

Answer: Option B

No explanation is given for this question. Let's Discuss on Board