ABC is a triangle, PQ is line segment intersecting AB is P and AC in Q and PQ || BC. The ratio of AP : BP = 3 : 5 and length of PQ is 18 cm. The length of BC is:
A. 28 cm
B. 48 cm
C. 84 cm
D. 42 cm
Answer: Option B
Solution (By Examveda Team)

∵ PQ || BC
So ∠AQP = ∠ACB = α
and
∠APQ = ∠ABC = β
So, ΔABC and ΔAPQ
$$\eqalign{ & \frac{{AP}}{{AB}} = \frac{{PQ}}{{BC}} \cr & \frac{3}{8} = \frac{{PQ}}{{BC}} \cr & \frac{3}{8} = \frac{{18}}{{BC}} \cr & BC = 48\,{\text{cm}} \cr} $$
Related Questions on Triangles
If ABC and PQR are similar triangles in which ∠A = 47° and ∠Q = 83°, then ∠C is:
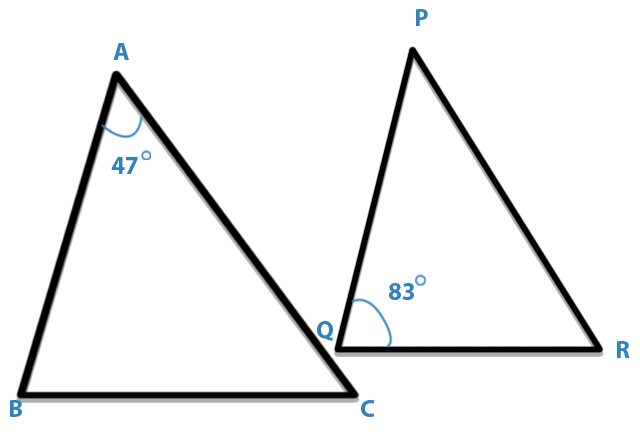
A. 50°
B. 70°
C. 60°
D. 80°
In the following figure which of the following statements is true?
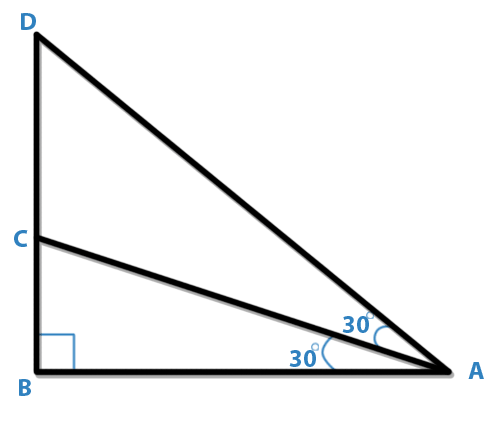
A. AB = BD
B. AC = CD
C. BC + CD
D. AD < Cd

Join The Discussion