In triangle PQR length of the side QR is less than twice the length of the side PQ by 2 cm. Length of the side PR exceeds the length of the side PQ by 10 cm. The perimeter is 40 cm. The length of the smallest side of the triangle PQR is :
A. 6 cm
B. 8 cm
C. 7 cm
D. 10 cm
Answer: Option B
Solution(By Examveda Team)
In δ PQR, QR + 2 = 2PQ QR = 2PQ - 2 - - - - - - - (1) PR = PQ + 10 - - - - - - (2)Perimeter = 40 m PQ + QR + Rp = 40 Putting the value of PQ and QR from equation (1) and (2), PQ + 2PQ - 2 + PQ + 10 = 40 4PQ = 32 PQ = 8 cm which is the smallest side of the triangle.
This Question Belongs to Arithmetic Ability >> Triangles
Join The Discussion
Comments ( 1 )
Related Questions on Triangles
If ABC and PQR are similar triangles in which ∠A = 47° and ∠Q = 83°, then ∠C is:
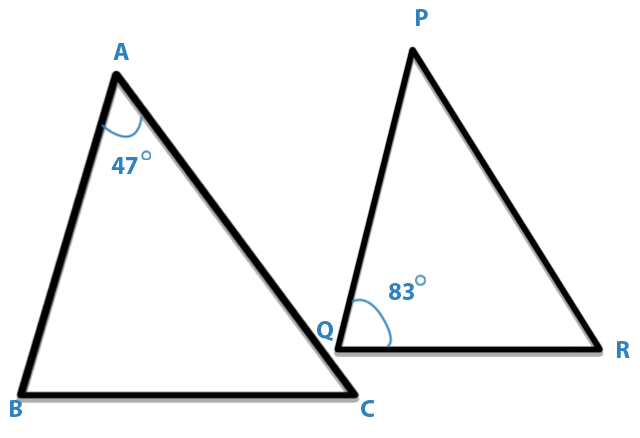
A. 50°
B. 70°
C. 60°
D. 80°
In the following figure which of the following statements is true?
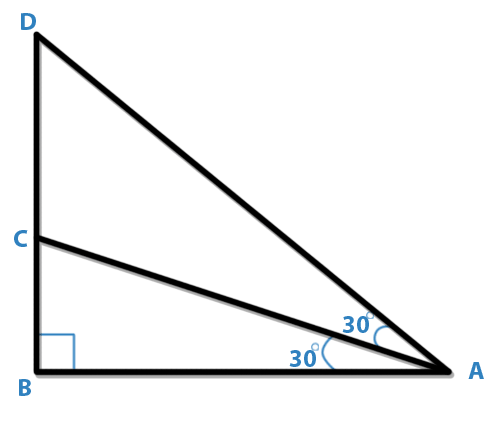
A. AB = BD
B. AC = CD
C. BC + CD
D. AD < Cd
In a Triangle PQR,
Length of PQ = x cm,
Length of PR = y cm,
Length of QR = z cm
Length of the side QR is less than twice the length of the side PQ by 2 cm
i.e., z = 2x - 2
Length of the side PR exceeds the length of the side PQ by 10 cm
i.e., y = x + 10
x + y + z = 40
x + (x+10) + (2x-2) = 40
4x + 8 = 40
4x = 40 - 8 = 32
x = 32/4 = 8 cm
x = 8 cm
y = x + 10 = 10 + 8 = 18 cm
z = 2x - 2 = (2 * 8) - 2 = 16 - 2 = 14 cm
Smallest side of the triangle = x = 8 cms