ABC is an isosceles triangle with AB = AC, A circle through B touching AC at the middle point intersects AB at P. Then AP : AB is:
A. 4 : 1
B. 2 : 3
C. 3 : 5
D. 1 : 4
Answer: Option D
Solution (By Examveda Team)
According to question,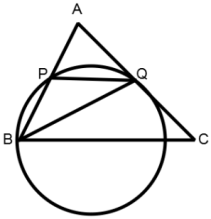
Let AB = AC = 2x
∵ AQ = QC = x
∴ AB is a secant
∴ AP × AB = AQ2
AP × 2x = x2
$$\eqalign{ & AP = \frac{x}{2} \cr & \frac{{AP}}{{AB}} = \frac{x}{{2 \times 2x}} = \frac{1}{4} \cr & \frac{{AP}}{{AB}} = \frac{1}{4} \cr & AP:AB = 1:4 \cr} $$
Related Questions on Triangles
If ABC and PQR are similar triangles in which ∠A = 47° and ∠Q = 83°, then ∠C is:
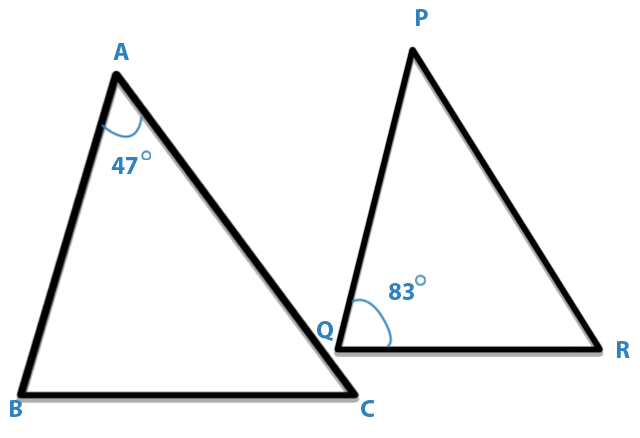
A. 50°
B. 70°
C. 60°
D. 80°
In the following figure which of the following statements is true?
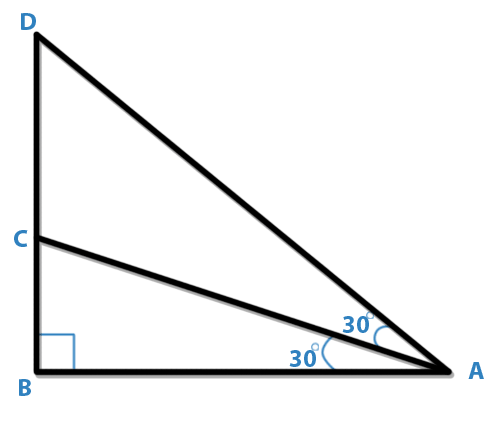
A. AB = BD
B. AC = CD
C. BC + CD
D. AD < Cd

Join The Discussion