G is the centroid of the equilateral ΔABC. If AB = 10 cm then length of AG is ?
A. $$\frac{{5\sqrt 3 }}{3}\,cm$$
B. $$\frac{{10\sqrt 3 }}{3}\,cm$$
C. $$5\sqrt 3 \,cm$$
D. $$10\sqrt 3 \,cm$$
Answer: Option B
Solution (By Examveda Team)
According to question,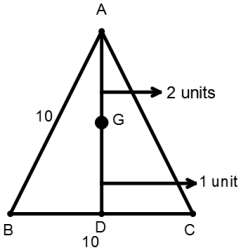
Given :
AB = BC = CA = 10 cm
G = Centroid
AG = 2 units
GD = 1 unit
AD = 3 units = Height
As we know that the height of the equilateral triangle is
$$\eqalign{ & = \frac{{\sqrt 3 }}{2} \times 10 = 5\sqrt 3 \cr & \therefore 3\,{\text{units}} = 5\sqrt 3 \cr & \,\,\,\,\,\,1\,{\text{unit}} = \frac{{5\sqrt 3 }}{3} \cr & \,\,\,\,\,\,2\,{\text{units}} = \frac{{5\sqrt 3 }}{3} \times 2 \cr & \,\,\,\,\,\,2\,{\text{units}} = \frac{{10\sqrt 3 }}{3} \cr & \therefore {\text{AG}} = \frac{{10\sqrt 3 }}{3}\,cm \cr} $$
Related Questions on Triangles
If ABC and PQR are similar triangles in which ∠A = 47° and ∠Q = 83°, then ∠C is:
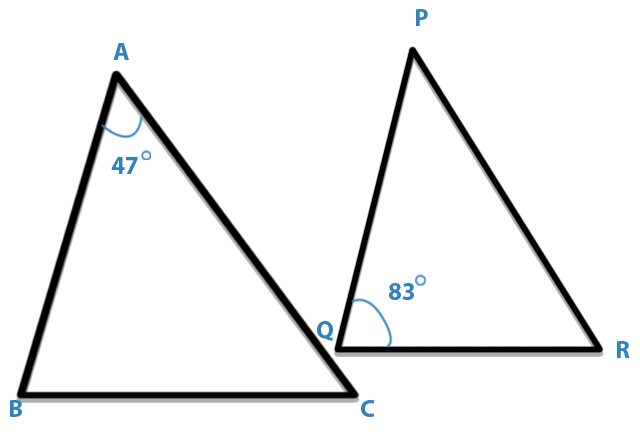
A. 50°
B. 70°
C. 60°
D. 80°
In the following figure which of the following statements is true?
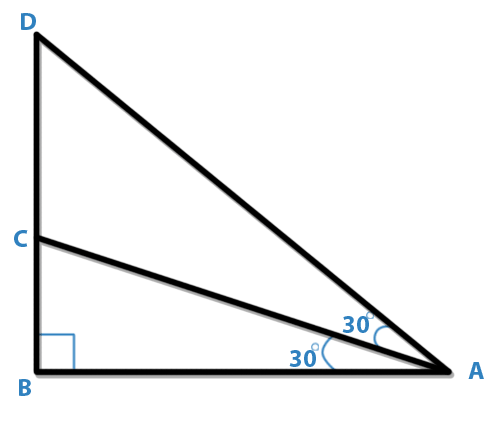
A. AB = BD
B. AC = CD
C. BC + CD
D. AD < Cd

Join The Discussion