In a triangle ABC, the internal bisector of the angle A meets BC at D. If AB = 4, AC = 3 and ∠A = 60°, then length of AD is :
A. $$2\sqrt 3 $$
B. $$\frac{{12\sqrt 3 }}{7}$$
C. $$\frac{{15\sqrt 3 }}{8}$$
D. $$\frac{{6\sqrt 3 }}{7}$$
E. None of these
Answer: Option B
Solution(By Examveda Team)
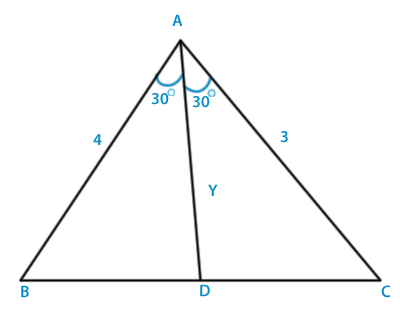
Let BC = x and Ad = y, then as per bisector theorem,
$$\frac{{{\text{BD}}}}{{{\text{DC}}}} = \frac{{{\text{AB}}}}{{{\text{AC}}}} = \frac{4}{3}$$
Hence, BD = $$\frac{{4{\text{x}}}}{7}$$ and DC = $$\frac{{3{\text{x}}}}{7}$$
Now, in ΔABD using cosine rule,
$$\cos {30^ \circ } = \frac{{{4^2} + {{\text{y}}^2} - {\frac{{16{{\text{x}}^2}}}{{49}}} }}{{2 \times 3 \times {\text{y}}}}$$
$${\text{or,}}\,4\sqrt {3{\text{y}}} = {16 + {{\text{y}}^2} - {\frac{{16{{\text{x}}^2}}}{{49}}} } $$ - - - - - - (i)
Similarly in ΔADC,
$$\cos {30^ \circ } = \frac{{{3^2} + {{\text{y}}^2} - {\frac{{9{{\text{x}}^2}}}{{49}}} }}{{2 \times 3 \times {\text{y}}}}$$
$${\text{or,}}\,3\sqrt {3{\text{y}}} = {9 + {{\text{y}}^2} - {\frac{{9{{\text{x}}^2}}}{{49}}} } $$ - - - - - - - - (ii)
From equation (i) and (ii), we get
$${\text{y}} = \frac{{12\sqrt 3 }}{7}$$
Join The Discussion
Comments ( 1 )
Related Questions on Triangles
If ABC and PQR are similar triangles in which ∠A = 47° and ∠Q = 83°, then ∠C is:
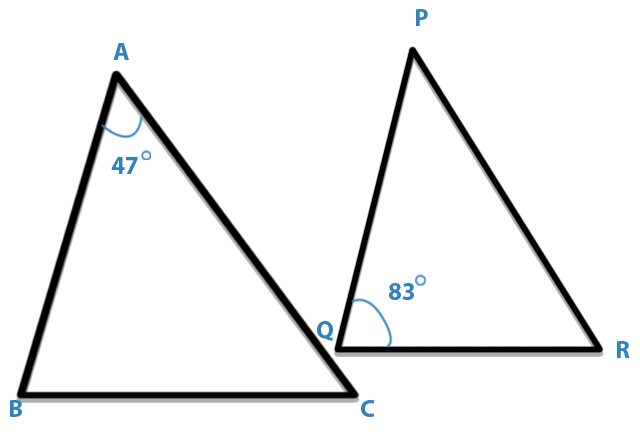
A. 50°
B. 70°
C. 60°
D. 80°
In the following figure which of the following statements is true?
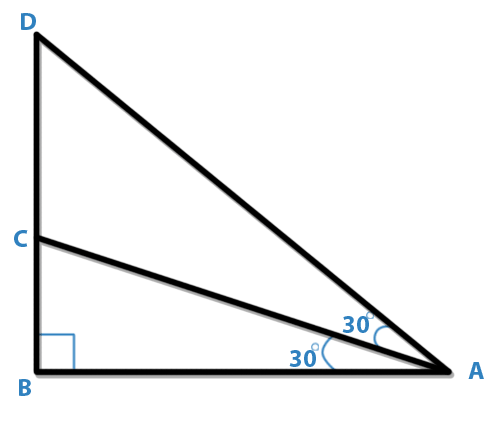
A. AB = BD
B. AC = CD
C. BC + CD
D. AD < Cd

How can we use cosine rule if angle ADB not 90? My doubt is, if we use cos or sin then one of the angle must be 90. Pls help me with my doubt