In ΔPQR, PS is the bisector of ∠P and PT ⊥ OR, then ∠TPS is equal to:
A. ∠Q + ∠R
B. 90° + $$\frac{1}{2}$$ ∠Q
C. 90° - $$\frac{1}{2}$$ ∠R
D. $$\frac{1}{2}$$ (∠Q - ∠R)
Answer: Option D
Solution(By Examveda Team)
∠1 + ∠2 = ∠3 [PS is bisector.] - - - - - - (1) ∠Q = 90° - ∠1 ∠R = 90° -∠2 - ∠3 So, ∠Q - ∠R = (90° - ∠1) - (90° - ∠2 - ∠3) ∠Q - ∠R = ∠2 + ∠3 - ∠1 ∠Q - ∠R = ∠2 + (∠1 + ∠2) -∠1[using equation 1] ∠Q - ∠R = 2∠2 $$\frac{1}{2}$$ × (∠Q - ∠R) = ∠TPSJoin The Discussion
Comments ( 4 )
Related Questions on Triangles
If ABC and PQR are similar triangles in which ∠A = 47° and ∠Q = 83°, then ∠C is:
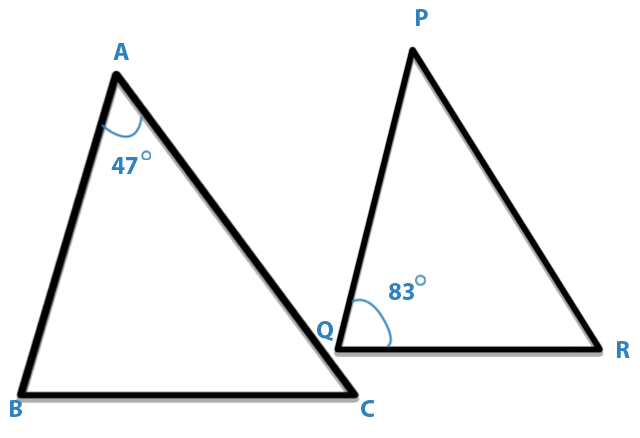
A. 50°
B. 70°
C. 60°
D. 80°
In the following figure which of the following statements is true?
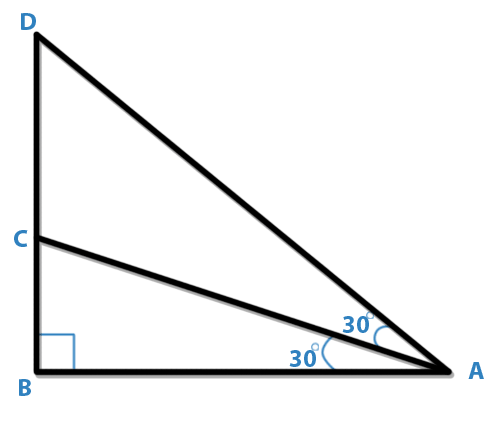
A. AB = BD
B. AC = CD
C. BC + CD
D. AD < Cd

without diagram it seems hard.
Plz explain
please post the diagram for this problem
can you draw the diagram for this?