In ΔABC, AD is the internal bisector of ∠A, meeting the side BC at D. If BD = 5 cm, BC = 7.5 cm, then AB : AC is
A. 2 : 1
B. 1 : 2
C. 4 : 5
D. 3 : 5
Answer: Option A
Solution (By Examveda Team)
According to question,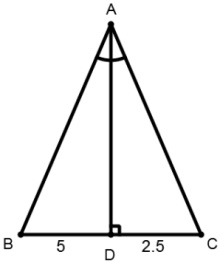
By internal bisector property
$$\eqalign{ & \frac{{AB}}{{AC}} = \frac{{BD}}{{DC}} \cr & \frac{{AB}}{{AC}} = \frac{5}{{2.5}} \cr & \frac{{AB}}{{AC}} = \frac{2}{1} \cr & \therefore AB:AC = 2:1 \cr} $$
Join The Discussion
Comments (1)
Related Questions on Triangles
If ABC and PQR are similar triangles in which ∠A = 47° and ∠Q = 83°, then ∠C is:
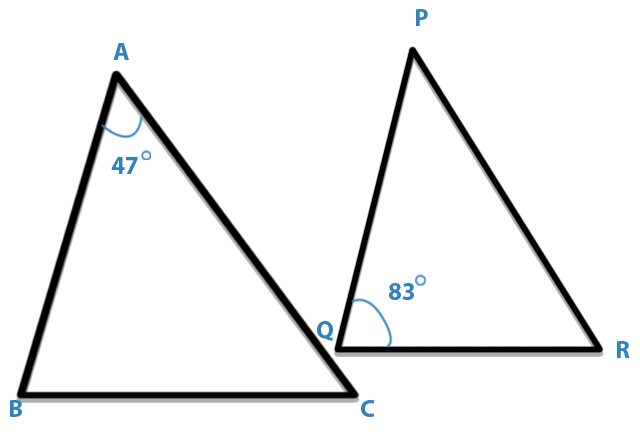
A. 50°
B. 70°
C. 60°
D. 80°
In the following figure which of the following statements is true?
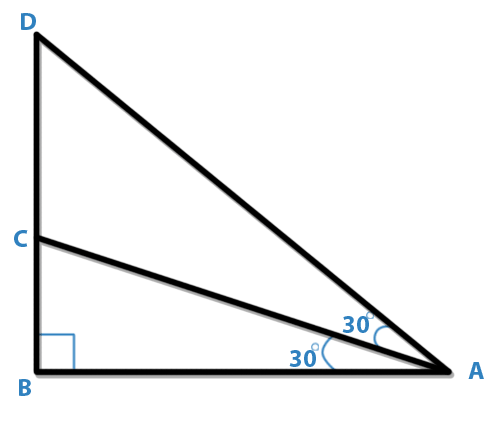
A. AB = BD
B. AC = CD
C. BC + CD
D. AD < Cd

Internal bisector of a angle, bisect the opposite side of the angle, hence BD=CD