81. The unit step response y(t) of a linear system is defined as y(t) = (1 - 3e-t + 3e-2t)u(t)
For the system function, the frequency at which the forced response becomes zero is:
For the system function, the frequency at which the forced response becomes zero is:
82. The region of the z plane for which $$\left| {\frac{{z - a}}{{z + a}}} \right| = 1\,\,\left( {\operatorname{Re} a \ne 0} \right)$$ is
83. Ideal frequency selective filters are
84. Consider a real-valued base-band signal x(t), band limited to 10 kHz. The Nyquist rate for the signal $${\text{y}}\left( {\text{t}} \right) = {\text{x}}\left( {\text{t}} \right){\text{x}}\left( {1 + \frac{{\text{t}}}{2}} \right)$$ is
85. The number of complex multiplications required to calculate N-point DFT using radix-2 FFT algorithm is
86. Consider the signal x(t) = cos (2πf0t). Its Hilbert transform is
87. In the case of a random variable dealing with non-deterministic signals
88. Laplace transform of the given signal x(t) = u(t - 2) is
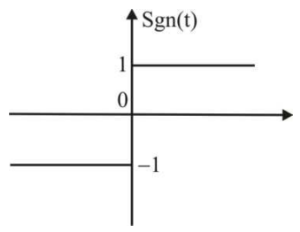
89. The Fourier transform of the function Sgn(t) defined in the Figure is

90. If xin(t) = sin(2$$\pi $$ × 4000t) + 0.75sin(2$$\pi $$ × 5000t + $$\frac{\pi }{4}$$) is sampled with Fs = 16000 Hz. Calculate X(0) if $$X\left( m \right) = \sum\nolimits_{n = 0}^{N - 1} {x\left( n \right){e^{ - \frac{{j2\pi nm}}{N}}}} .$$ When N = 8, where x(n) = xin(nts)
Read More Section(Signal Processing)
Each Section contains maximum 100 MCQs question on Signal Processing. To get more questions visit other sections.
